在计算机科学中，数据结构的选择直接影响到算法的效率。而理解时间复杂度是评估算法效率的关键一步。时间复杂度是一个函数，用于描述算法执行所需的时间与输入规模之间的关系。本文将详细介绍时间复杂度的计算方法及相关公式，帮助读者更好地理解这一概念。

一、时间复杂度的基本概念

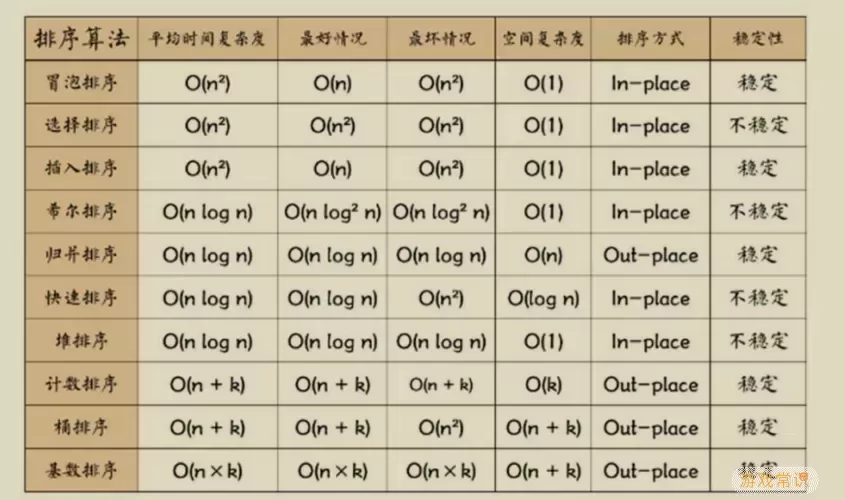
时间复杂度是通过输入数据规模n来衡量算法运行时间的一个指标。它通常使用“大O符号”表示，表明运行时间的上界。例如，O(1)、O(n)、O(n^2)等，分别代表算法的运行时间是常数级、线性级和平方级。

二、时间复杂度的分类

时间复杂度可以分为以下几类：

常数时间复杂度 O(1)：无论输入规模如何，算法的执行时间始终保持不变。

线性时间复杂度 O(n)：算法的执行时间与输入数据规模成正比。

平方时间复杂度 O(n^2)：算法的执行时间与输入数据规模的平方成正比，常见于嵌套循环。

对数时间复杂度 O(log n)：算法的执行时间与输入规模的对数成正比，常见于二分查找。

线性对数时间复杂度 O(n log n)：常出现在最优的排序算法中，如归并排序和快速排序。

三、时间复杂度的计算方法

计算时间复杂度的核心在于分析算法关键操作的执行次数。以下是几种常见的计算方法：

1. 逐步分析法

逐步分析法是最直观的计算方法。通过对算法中的每个基本操作进行逐一分析，累加其执行次数，从而得出时间复杂度。例如，对于一个简单的循环：

for (int i = 0; i < n; i++) { // 进行常数级操作 }

此段代码中，循环执行n次，因此时间复杂度为O(n)。

2. 划分法

划分法适用于递归算法。通过将问题划分成更小的子问题，利用递归关系来描述时间复杂度。例如，快速排序的时间复杂度通常用递归关系T(n) = T(k) + T(n-k) + O(n)来表示，其中O(n)是合并的时间。

3. 取上界法

在某些情况下，可能需要对算法进行优化或考虑最坏情况。此时，可以根据算法的最坏情况取上界来估算时间复杂度。例如，对于双重循环，其中外层循环执行n次，内层循环执行n次，则总的复杂度为O(n^2)。

四、时间复杂度的常用公式

在计算时间复杂度时，以下公式可以帮助提高效率：

常量操作的复杂度： O(c) = O(1)，其中c为常数。

加法法则： 如果算法由几个部分组成，时间复杂度为O(f(n) + g(n)) = O(max(f(n), g(n)))。

乘法法则： 如果算法包含嵌套循环，时间复杂度为O(f(n) * g(n))。

取对数： O(log a(b)) = O(log b / log a)，这在某些情况下可以简化复杂度。

五、总结

时间复杂度是评估算法效率的重要工具，通过理解和运用计算方法及公式，开发人员可以更好地选择数据结构和算法，提升程序的执行效率。深入研究时间复杂度，不仅有助于解决实际问题，也能为算法的设计和实现提供理论基础。希望本文能帮助读者更清楚地掌握时间复杂度的计算方法及其应用。